Maryam Akmal
Center for Global Development
Blog
At what grade are children taught how to do division? Figure 1 below plots the fraction of children in India, Kenya, Pakistan, and Uganda who can divide a larger number by a one-digit number, with possible remainders (e.g., 659/4), at various grade levels. From this graph, you cannot really tell when division is taught.
The striking thing about this graph is that starting at Grade 2/3, the learning profile is roughly linear as the slope starts to increase, until the slope plateaus as mastery reaches 80 or 90 percent (around Grades 7 or 8 in Kenya and Uganda, Grade 9 in Pakistan, and far too late in India).
Figure 1. When do children master simple division?
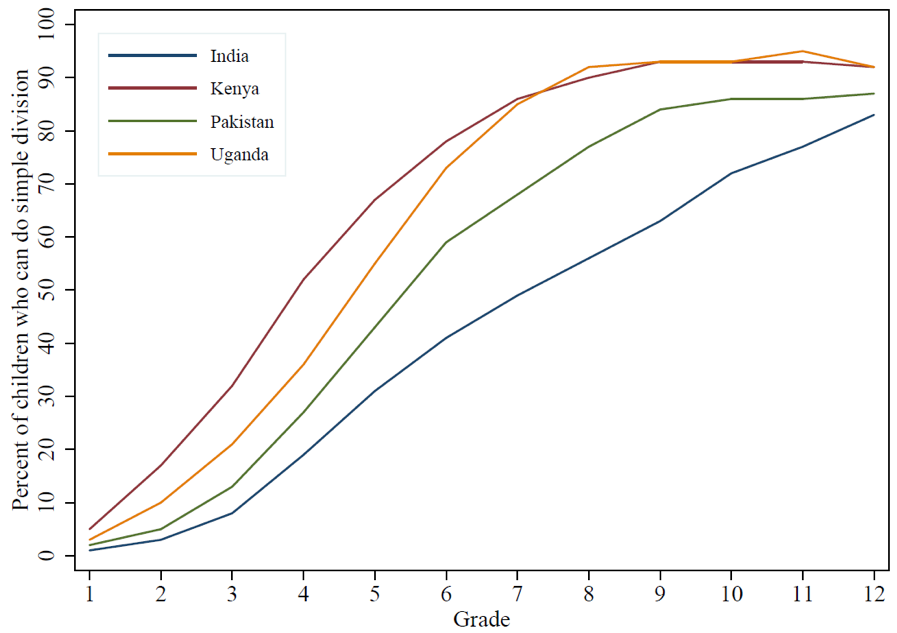
Source: Author’s calculations based on ASER and Uwezo data for all available years.
Let’s look closely at India, which represents a sample of more than 2.8 million children in the ASER data. In Grades 1-2 only 4 percent of the children know division, which isn’t surprising because they aren’t taught division at that grade level. Double that number know how to do division in Grade 3. Between Grades 3 and 4, there is only an 11 percentage point jump in those who can do simple division, and between Grades 4 and 5, the jump is 12 percentage points. Grade 5 onwards, the jumps are similar in magnitude: 10 percentage points from Grades 5-6, 8 percentage points from Grades 6-7, and 7 percentage points from Grades 8-9 and so on until the learning profile plateaus. If the concept of division is meant to be mastered at the fourth grade level, then why do we see an incremental increase in the number of children who can do division from grade to grade (apart from the modest figures you would expect to be getting remedial tuition)? In fact, the total overall improvement from Grades 1-6 seems to be similar to the improvement over Grades 6-12—which is far past when children are expected to learn one-digit division.
Figure 2. What is the gain in percent of children mastering simple division per grade in India?
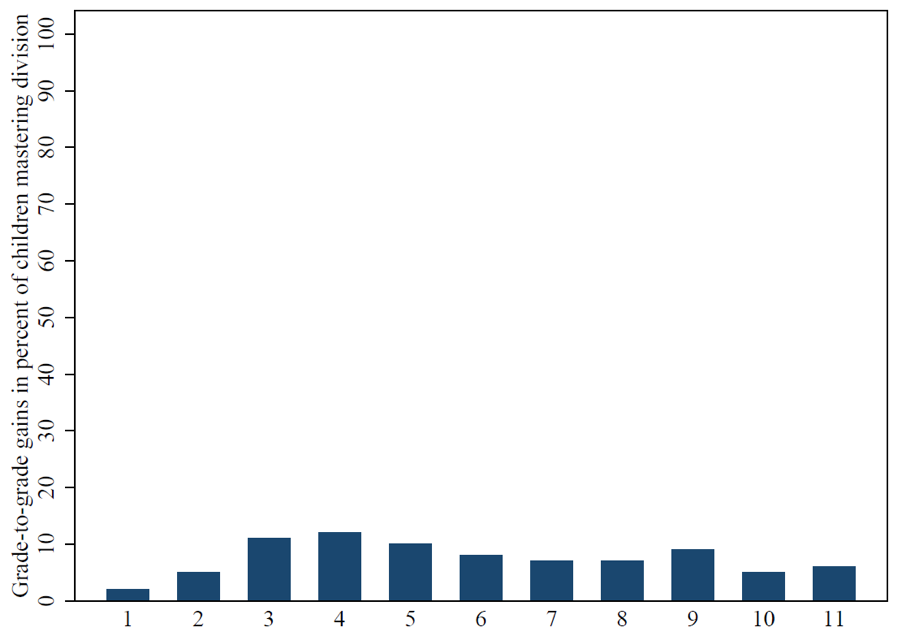
Why is this linearity of mastery level across a large number of grades (or equivalently, the rough constancy of the gain) a strange and potentially important fact? The popular notion about how schooling works—and, one could argue, the notion upon which the whole age-grade structure of schooling depends—is that one moves through a series of concepts that build on one another and masters them at the “grade appropriate” level. One would think that the mastery of individual arithmetic concepts taught in a curriculum sequenced by grade (e.g., in first grade we learn one-digit addition, in second grade we learn one-digit subtraction, in third grade we learn multiplication of one-digit numbers, in fourth grade we learn division by one-digit numbers, etc.) would be a series of steep “S” curves in which most children learn the concept in the grade in which it is taught in the curriculum.
For instance, what might it mean to say that division is a “fourth grade skill”? One thing that it could mean is that mastery before fourth grade is low (say around 20 percent in third grade). Since, division is taught in fourth grade, the mastery level would jump a lot in fourth grade so that something like 60 percent of the kids would learn that skill in fourth grade. Hence, end of fourth grade mastery would be around 80 percent. In fifth grade perhaps 20 percent would still need remediation to be able to master division. In higher grades, the mastery curve for simple division would plateau.
For each individual concept in a curriculum--particularly those concepts that build on one another (e.g., the concept of “place” in the representation of numbers base 10 is key to understanding algorithms for multiple-digit addition and subtraction; multiplication and subtraction of multiple digit numbers are necessary for multiple-digit division, etc.)--one would expect to see an S-curve in conceptual and algorithmic mastery, with the steepest part of the learning curve concentrated in the year that the concept was taught.
Figure 3 super-imposes a steep S-curve in mastery on the actual descriptive learning profiles of Figure 1. The grey line in Figure 3 is what we would expect the learning profile to look like in a system where division is taught and mastered by most students at the grade 4 level. The actual descriptive learning profiles just don’t have a distinctive “S.”
Figure 3. What should an S-curve for content mastered in Grade 4 look like?
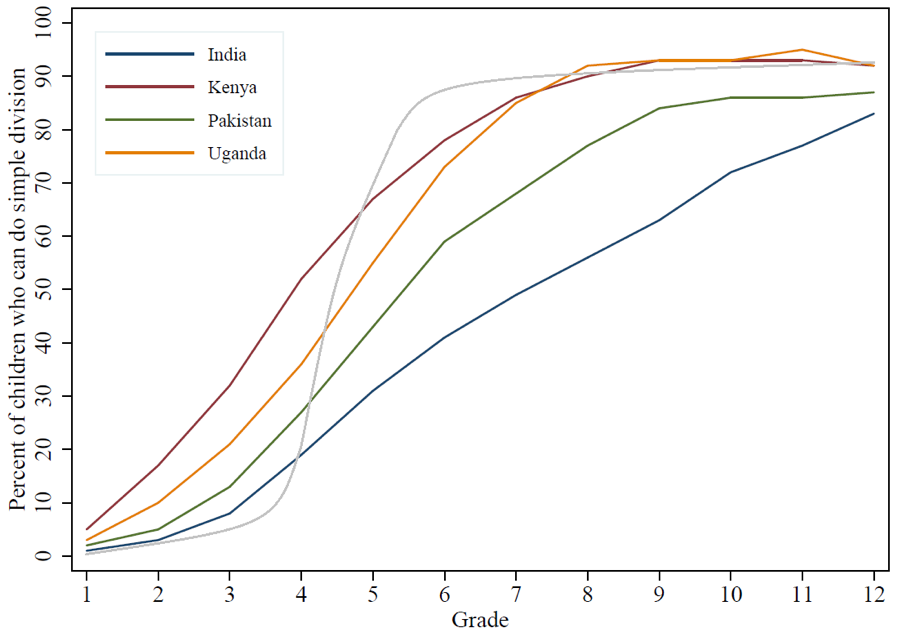
Source: Author’s calculations based on ASER and Uwezo data for all available years.
Figure 4. What would the gain in percent of children mastering simple division per grade in India look like if the learning profile followed an S-shape?
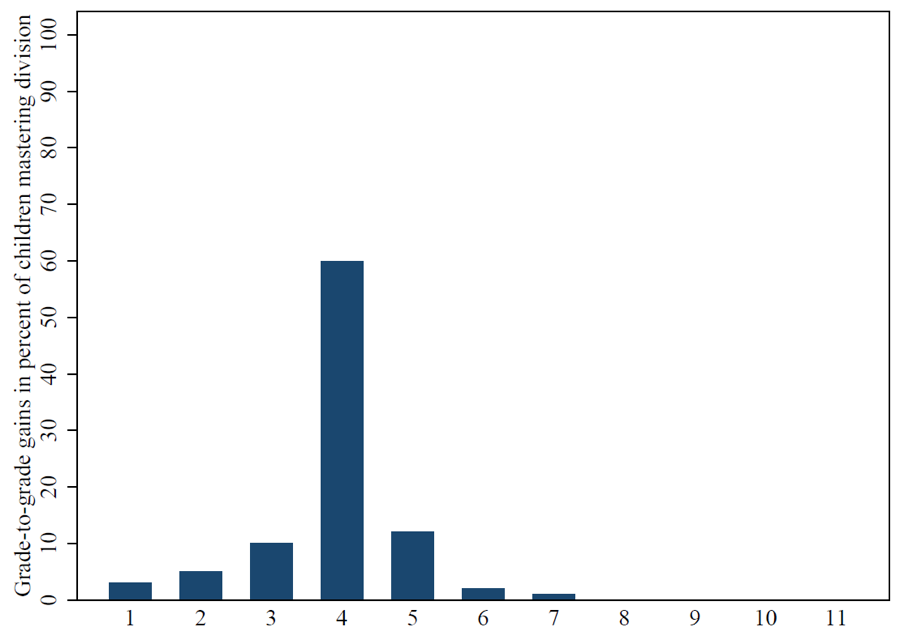
Note that there are two separate issues. One is that the learning profile is just very flat, so that grade completed doesn’t really predict content mastered at all (e.g., see this earlier blog post about Bangladesh using simple math concepts or more recent data from Indonesia or the DHS learning profiles for reading from low-performing countries like Ghana). The second issue is that the learning profile is reasonably steep but also quite linear.
Are these linear learning profiles strange or is that pretty much what the world is supposed to look like?Is it that math concepts are taught but there is lots of repetition and review so that “fourth-grade skill” just means “first time introduced,” but no one really expects a very steep “S” curve in the grade in which the concept is first taught?
What is clear is that without the “S” curve, every teacher is teaching to a very wide distribution of students’ skills in each grade and hence progress is going to be hard.
Nearly all modern schooling uses group-based classroom instruction in a sequenced curriculum. It assumes two things: 1) literacy and numeracy skills are cumulative and best mastered in a certain order, and 2), children in the same grade have relatively homogenous skills. But if the year in which a concept is taught doesn’t make any difference to the likelihood of concept mastery, then what is the advantage of the strict grade structure of classrooms?
In a previous blog post, Lant Pritchett showed that if learning per grade relative to dispersion of skills in the classroom is low (some have full mastery and some have zero), then knowing a child's grade doesn’t convey much about their actual knowledge and skills. If learning profiles are flat, as they are in large parts of South Asia, and sub-Saharan Africa, and if there is a large dispersion of skills mastered in a particular grade, then teaching based on a grade-based (and overambitious) curriculum that assumes mastery of grade-level content may be ineffective in raising learning outcomes.
When student ability doesn’t match with the grade-based curricular pace, teaching at the “skill-level” rather than “grade-level” has been shown to improve learning in India and Kenya. Structural changes in the organization of teaching and learning using simple innovations such as Teaching at the Right Level (TaRL) could help more children master basic literacy and numeracy. A pivot to effective teaching and learning will inevitably require deeper thinking about the basics of how schools organize instruction.
RISE blog posts and podcasts reflect the views of the authors and do not necessarily represent the views of the organisation or our funders.